Takeoff Distance

Typically, at this stage of design, the \(W/S\) and \(W/P\) required for a certain takeoff distance is determined using the takeoff parameter (TOP), which is defined as

\[ \text{TOP} = \frac{ \bigg( \dfrac{W}{S} \bigg)_{TO} \bigg( \dfrac{W}{P} \bigg)_{TO} }{ \sigma C_{L_{max_{TO}}} }, \]

where \(\sigma\) is the ratio of the density at the takeoff altitude to the sea-level. Most aircraft design books will provide a relation between \(\text{TOP}\) and takeoff ground roll or takeoff distance requried to clear an obstacle based on historical data.

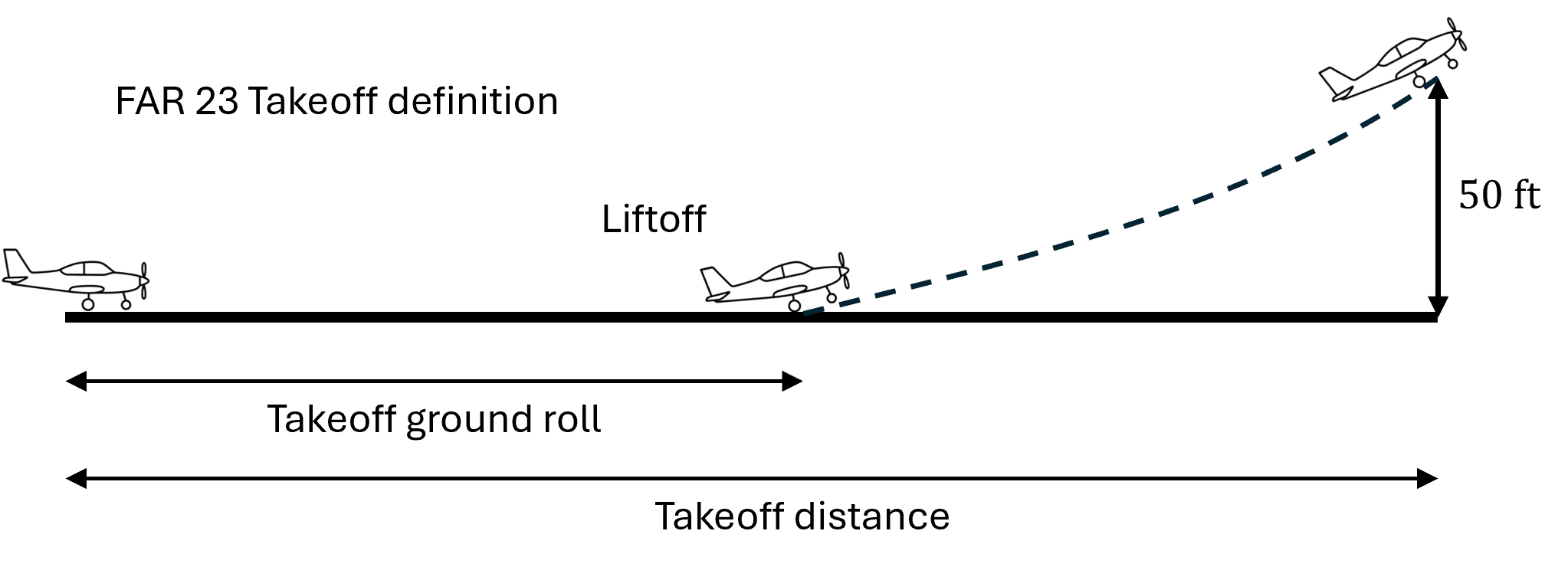
According to mission specifications, the example aircraft needs to takeoff within 1500 ft of ground roll. Additionally, it should also be able to climb to a distance of 50’ above takeoff surface according to CFR Part 23.2115. Schematically, it can be represented as

In this section, the TOP relation provided in the Section 3.1 of Roskam Part 1 is used, which is given by

\[ S_{TGR} = 4.9 \text{ } \text{TOP}_{23} + 0.009 \text{ } \text{TOP}_{23}^2, \]

where \(S_{TGR}\) is the required takeoff ground roll and \(\text{TOP}_{23}\) denotes TOP for FAR 23 airplanes.

NOTE: In the above equation, the \(S_{TGR}\) should be in feets, \(W/P\) should be in lbs/hp, and \(W/S\) should be in lbs/\(\text{ft}^2\)

The \(\text{TOP}_{23}\) can be solved from above quadratic equation and substituted into \(\text{TOP}\) equation to obtain

\[ \frac{ \bigg( \dfrac{W}{S} \bigg)_{TO} \bigg( \dfrac{W}{P} \bigg)_{TO} }{ \sigma C_{L_{max_{TO}}} } \leq \text{TOP}_{23}. \]

This inequality relation can be used to determine various combinations of \(W/S\) and \(W/P\) that satisfy the takeoff ground roll requirement for FAR 23 airplanes.

Below code plots the takeoff requirement for the example aircraft and highlights the feasible region:

import numpy as np
import matplotlib.pyplot as plt

s_tgr = 1500 # ft
sigma = 1 # since sealevel conditions
CL_max_to = 1.8

# coeff of quadratic eq
a = 0.009
b = 4.9
c = -s_tgr

# TOP solution
top_23 = (-b + np.sqrt(b**2 - 4*a*c)) / 2 / a # other solution will be negative

# W/S amd W/P values
num_pts = 500
wing_loading = np.linspace(5, 50, num_pts) # lb/ft^2
power_loading = np.linspace(5, 30, num_pts) # lb/hp
X, Y = np.meshgrid(wing_loading, power_loading)

takeoff_req = X * Y / sigma / CL_max_to - top_23

# Plotting
fs = 12 # fontsize

fig, ax = plt.subplots()
ax.contour(X, Y, takeoff_req, colors="k", levels=[0])
ax.contourf(wing_loading, power_loading, takeoff_req<=0, colors="r", levels=[0.5,1], alpha=0.5)
ax.annotate("Feasible", (17,12), fontsize=14, va="center", ha="center")
ax.set_xlabel("Wing Loading ($W/S$) [lbs/$ft^2$]", fontsize=fs)
ax.set_ylabel("Power Loading ($W/P$) [lbs/hp]", fontsize=fs)
ax.set_title("Takeoff distance requirement")
ax.tick_params(axis='both', labelsize=fs-2)
plt.tight_layout()

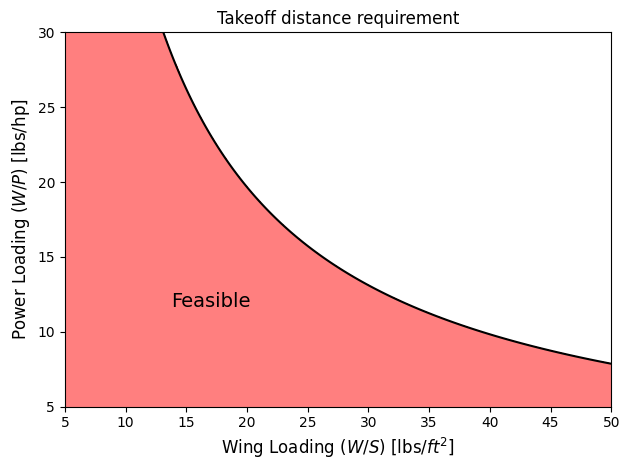
So, any point within this red feasbile region will be able to satisfy the takeoff requirement.