Takeoff#
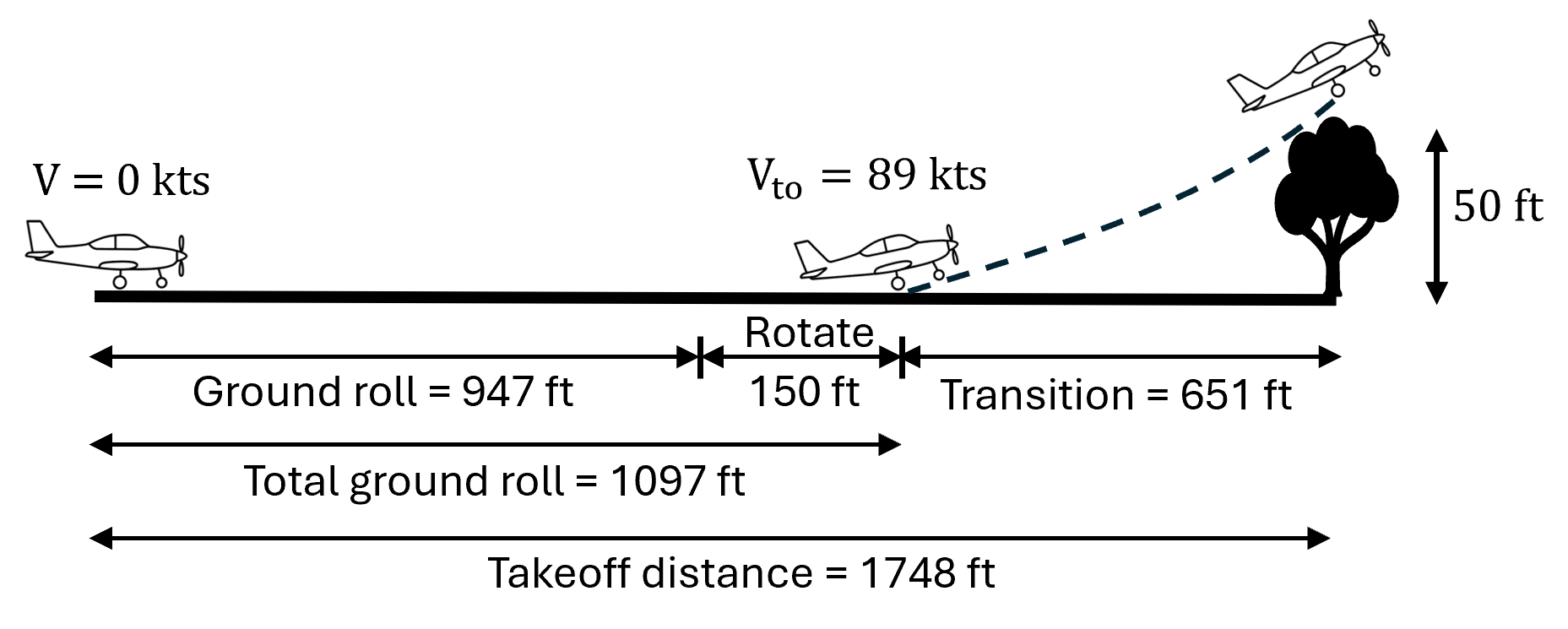
This section performs takeoff analysis for the example airplane using the method described in Raymer Section 17.8. The takeoff segment is divided into four parts - ground roll, rotation, transition to climb, and climb over obstacle. Refer to Figure 17.18 in Raymer for a visual depiction of these phases. Hence, total takeoff distance \(S_{to}\) is defined as
where \(S_{g}\) is the ground roll, \(S_{r}\) is the distance travelled during rotation, \(S_{tr}\) is the horizontal distance covered during transiting to climb, and \(S_c\) is the horizontal distance travelled before clearing the obstacle. Note that the total ground roll distance \(S_{gr}\) will be summation of \(S_g\) and \(S_r\). The following sub-sections compute the distance traveled in each phase.
Ground roll#
The ground roll distance \(S_g\) can be estimated using (equation 17.102, Raymer)
where \(K_a\) and \(K_t\) are defined as (equation 17.103 and 17.104, Raymer)
The \(T\) is the thrust computed using the average velocity during the ground roll phase, \(\mu\) is the rolling resistance coefficient and \(W\) is the takeoff weight. The \(g\) refers to acceleration due to gravity, \(C_L\) is the lift coefficient based on the angle of attack experienced by the plane on ground, and \(C_{D_0}\) is the parasitic drag coefficient in takeoff configuration. The takeoff velocity \(V_{to}\) is usually 1.1 times the stall speed, computed with takeoff flaps settings. The average velocity used for computing \(T\) is usually \(1/\sqrt{2}\) times \(V_{to}\).
Below block computes the takeoff speed \(V_{to}\) and the thrust \(T\):
# Parameters
wing_loading = 40 # lbs/sq ft
rho = 0.00237717 # slugs/cu ft, sea-level
CLmax_TO = 1.8
prop_eff = 0.8
P = 298 # hp, takeoff power
Vto = 1.1 * ( wing_loading * 2 / rho / CLmax_TO )**0.5
print(f"Takeoff speed: {Vto:.0f} ft/s")
T = 550 * P * prop_eff / 0.707 / Vto
T = 0.92 * T # installation loss
T_avg = 2*T # lbs
print(f"Average thrust during TO: {T_avg:.0f} lbs")
Takeoff speed: 150 ft/s
Average thrust during TO: 2269 lbs
Below code block computes ground roll distance:
import numpy as np
A = 8
e = 0.81 - 0.05 # in TO conditions
g = 32.174 # ft/s^2
mu = 0.04 # Raymer Table 17.1
W = 0.99 * 5374 # lbs
CD0 = 0.03363 + 0.024011 # TO conditions
CL = 0.6 # TO lift curve with wing incidence of 2 deg
# K in drag model
K = 1/np.pi/A/e
h = 4 # ft, height of wing above ground
b = 33 # ft, wing span
Keff = K * ( 33 * (h/b)**1.5 / ( 1 + 33 * (h/b)**1.5 ) ) # eq 12.60, Raymer
# ground roll distance
KT = (T_avg/W) - mu
KA = rho / 2 / wing_loading * (mu*CL - CD0 - Keff*CL**2)
Sg = np.log( 1 + KA/KT*Vto**2 ) / 2 / g / KA
print(f"Ground roll distance: {Sg:.0f} ft")
Ground roll distance: 947 ft
Rotation#
The distance covered during rotation depends on the pilot. However, it can be estimated using the takeoff speed and time for rotation, assuming that there is no acceleration in this phase. For small planes, it can be assumed that it takes about 1 sec for rotation. Below code block computes \(S_r\) and total ground roll \(S_{gr}\):
t_rotation = 1 # sec
Sr = Vto * t_rotation
print(f"Distance travelled during rotation: {Sr:.0f} ft")
Sgr = Sg + Sr
print(f"Total ground roll: {Sgr:.0f} ft")
Distance travelled during rotation: 150 ft
Total ground roll: 1097 ft
Based on the calculations, the total ground roll for the example airplane is less than the requried distance of 1500 ft.
Transition and Climb#
During transition, airplane accelerates from takeoff speed (1.1 times stall speed) to climb speed (1.2 times stall speed), and hence, the average speed during transition \(V_{tr}\) will be about 1.15 times stall speed. The path of the airplane is approximated as a circular arc whose radius is given as (equation 17.107, Raymer)
The climb angle at the end of this phase is computed using (equation 17.108, Raymer)
where the average \(T\) is computed using \(V_{tr}\) and the average \(L/D\) is computed using 90% of the maximum \(L/D\) with takeoff flaps. Using this radius \(R\) and climb angle \(\gamma_{climb}\), horizontal and vertical distance traveled by the airplane during this phase can be computed. First, vertical distance is computed using (equation 17.110, Raymer)
If \(h_{tr}\) is less than the obstacle height \(h_{obs}\) (50 ft in this case), then \(S_{tr}\) is computed using (equation 17.109, Raymer)
If \(h_{tr}\) is more than the obstacle height \(h_{obs}\), then \(S_{tr}\) is computed using (equation 17.111, Raymer)
Moreover, the climb distance \(S_c\) will also be zero since airplane has traveled the required vertical distance of \(h_{obs}\).
Below code block computes \(\gamma_{climb}\) and \(h_{tr}\):
# Transition speed
Vtr = 1.15 * Vto / 1.1 # ft/s
# Radius
R = Vtr**2 / 0.2 / g # ft
# Thrust
T = 550 * P * prop_eff / Vtr
T = 0.92 * T # installation loss
T_transition = 2 * T # lbs
# Climb angle
CL_tr = 0.9*CLmax_TO
L_by_D = CL_tr / ( CD0 + K*CL_tr**2 )
W = 0.985 * 5374 # lbs
climb_gamma = np.arcsin( T_transition/W - 1/L_by_D ) * 180 / np.pi # deg
print(f"Climb angle: {climb_gamma:.0f} deg")
# Vertical distance
htr = R * (1 - np.cos(np.deg2rad(climb_gamma))) # ft
print(f"Vertical height gained: {htr:.0f} ft")
Climb angle: 10 deg
Vertical height gained: 56 ft
Based on the above calculcations, the vertical height is more than the obstacle of 50 ft. Hence, \(S_{tr}\) will be computed using equation 17.111 (Raymer) and \(S_c\) will zero. Below block computes \(S_{tr}\) and \(S_{c}\):
Str = ( R**2 - (R - htr)**2 )**0.5
print(f"Horizonal distance traveled during transition: {Str:.0f} ft")
Sc = 0
Horizonal distance traveled during transition: 651 ft
\(S_{to}\)#
The final takeoff distance is just the sum of the individual components. Below code block computes \(S_{to}\):
Sto = Sg + Sr + Str + Sc
print(f"Total takeoff distance: {Sto:.0f} ft")
Total takeoff distance: 1749 ft
Below image summarizes the final result from the takeoff analysis:
This concludes the takeoff analysis, next section is about landing distance.