Numerical Differentiation

Computing derivatives is a common task in many numerical techniques. There are many ways to do this such such as finite difference approximations, symbolic differentiation, and automatic differentiation. We will focus on finite difference approximations only.

Example: Use forward, backward, and central difference approximation for estimating the first derivative of

\[ f(x) = -0.1x^{4} - 0.15x^{3} - 0.5x^{2} - 0.25x + 1.25 \]

at \(x = 0.5\) using a step size \(h = 0.5\).

Solution:

Following block of code imports required packages.

import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np

Following block of code defines function for computing various approximation and true value of derivative.

def forward_diff(x,h,func):
    """
        Function for computing forward difference.
        Input:
        x - input at which derivative is desired
        h - step size
        func - python function which should return function value based on x.
    """
    slope = (func(x+h) - func(x)) / h
    return slope

def backward_diff(x,h,func):
    """
        Function for computing backward difference.
        Input:
        x - input at which derivative is desired
        h - step size
        func - python function which should return function value based on x.
    """
    slope = (func(x) - func(x-h)) / h
    return slope

def central_diff(x,h,func):
    """
        Function for computing central difference.
        Input:
        x - input at which derivative is desired
        h - step size
        func - python function which should return function value based on x.
    """
    slope = (func(x+h) - func(x-h)) /2/h
    return slope

def true_function(x):
    """
        Function which returns value of desired function at input x.
    """
    return -0.1*x**4 - 0.15*x**3 - 0.5*x**2 - 0.25*x + 1.25

def true_derivative(x):
    """
        Returns true derivative of function at input x.
    """
    return -0.4*x**3 - 0.45*x**2 - x - 0.25

Following block of code computes true and approximate value of derivate, and the error in the estimation using the functions defined in previous block

# Few vairables
x = 0.5
h = 0.5

# True value
true_value = true_derivative(x)
print("True value: {}\n".format(true_value))

# Forward difference
approx_value = forward_diff(x,h,true_function)
print("Forward difference:")
print("Approx value: {}".format(approx_value))
print("True error: {}\n".format((true_value - approx_value)/true_value))

# Backward difference
approx_value = backward_diff(x,h,true_function)
print("Backward difference:")
print("Approx value: {}".format(approx_value))
print("True error: {}\n".format((true_value - approx_value)/true_value))

# Central difference
approx_value = central_diff(x,h,true_function)
print("Central difference:")
print("Approx value: {}".format(approx_value))
print("True error: {}".format((true_value - approx_value)/true_value))

True value: -0.9125

Forward difference:
Approx value: -1.45
True error: -0.589041095890411

Backward difference:
Approx value: -0.55
True error: 0.39726027397260266

Central difference:
Approx value: -1.0
True error: -0.09589041095890413

Now, we will check the variation of error based on the step size

def error_estimation(func,method,x,step_sizes):
    """
        Function to compute error in the estimation for various step sizes
        Input:
        func - function which returns value of desired function at input x
        method - function which returns derivative estimation at x
        x - value at which derivative is required
        step_sizes - 1d numpy array containing step sizes for derivative estimation
    """
    
    # Initializing error array
    error = np.zeros(len(step_sizes))
    
    # Computing error for the given step sizes
    for index, step in enumerate(step_sizes):
        true_value = true_derivative(x)
        approx_value = method(x,step,func)
        error[index] = abs((true_value - approx_value)/true_value)
    
    return error

# Value at which derivative is required
x = 0.5

# Calculating step sizes
initial_step = 0.5
num_steps = 60
step_sizes = np.zeros(num_steps)
for i in range(num_steps):
    step_sizes[i] = initial_step/(2**i)

error_forward_diff = error_estimation(true_function,forward_diff,x,step_sizes)
error_backward_diff = error_estimation(true_function,backward_diff,x,step_sizes)
error_central_diff = error_estimation(true_function,central_diff,x,step_sizes)

# Plotting the error variation with step sizes for different methods
fig, ax = plt.subplots()
ax.plot(step_sizes, error_forward_diff, label="Forward", marker='.')
ax.plot(step_sizes, error_backward_diff, label="Backward", marker='.')
ax.plot(step_sizes, error_central_diff, label="Central", marker='.')
ax.set_xscale('log')
ax.invert_xaxis()
ax.set_yscale('log')
ax.set_xlabel("Step size (h)")
ax.set_ylabel("Absolute value of true error")
ax.legend(loc="lower right")
ax.grid()

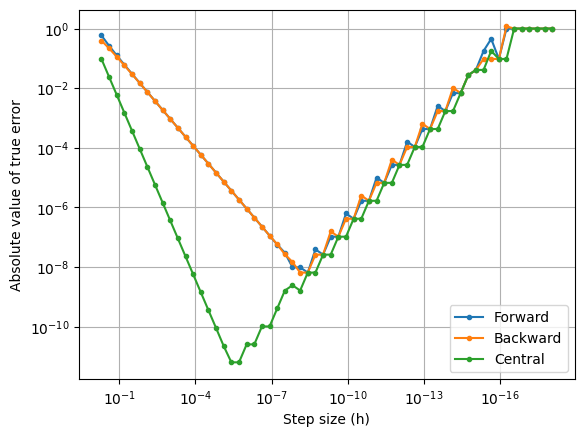
As seen in the plot above, error in all the methods starts to increase after a specific step size but central difference is more accurate than forward and backward difference. A more robust estimate of derivate can be obtained by using complex-step method.