Exploitation

This section implements pure exploitation process where the next infill point is obtained by minimizing the surrogate prediction. Below code imports required packages, defines modified branin function, and creates plotting data:

# Imports
import numpy as np
from smt.surrogate_models import KRG
from smt.sampling_methods import LHS, FullFactorial
import matplotlib.pyplot as plt
from pymoo.core.problem import Problem
from pymoo.algorithms.soo.nonconvex.de import DE
from pymoo.optimize import minimize
from pymoo.config import Config
Config.warnings['not_compiled'] = False

def modified_branin(x):

    dim = x.ndim

    if dim == 1:
        x = x.reshape(1, -1)

    x1 = x[:,0]
    x2 = x[:,1]

    a = 1.
    b = 5.1 / (4.*np.pi**2)
    c = 5. / np.pi
    r = 6.
    s = 10.
    t = 1. / (8.*np.pi)

    y = a * (x2 - b*x1**2 + c*x1 - r)**2 + s*(1-t)*np.cos(x1) + s + 5*x1

    if dim == 1:
        y = y.reshape(-1)

    return y

# Bounds
lb = np.array([-5, 0])
ub = np.array([10, 15])

# Plotting data
sampler = FullFactorial(xlimits=np.array( [[lb[0], ub[0]], [lb[1], ub[1]]] ))
num_plot = 400
xplot = sampler(num_plot)
yplot = modified_branin(xplot)

Differential evolution (DE) from pymoo is used for minimizing the surrogate model. Below code defines problem class and initializes DE. Note that the problem class uses surrogate model prediction instead of actual function.

# Problem class
class Exploitation(Problem):

    def __init__(self, sm):
        super().__init__(n_var=2, n_obj=1, n_constr=0, xl=lb, xu=ub)

        self.sm = sm # store the surrogate model

    def _evaluate(self, x, out, *args, **kwargs):

        out["F"] = self.sm.predict_values(x)

# Optimization algorithm
algorithm = DE(pop_size=100, CR=0.8, dither="vector")

Below block of code creates 5 training points and performs sequential sampling using exploitation. The maximum number of iterations is set to 15 and a convergence criterion is defined based on the change in true function value for infill points between two consecutive iterations.

sampler = LHS(xlimits=np.array( [[lb[0], ub[0]], [lb[1], ub[1]]] ), criterion='ese')

# Training data
num_train = 5
xtrain = sampler(num_train)
ytrain = modified_branin(xtrain)

# Variables
itr = 0
max_itr = 15
tol = 1e-3
delta_f = [1]
bounds = [(lb[0], ub[0]), (lb[1], ub[1])]
corr = 'squar_exp'
fs = 12

# Sequential sampling Loop
while itr < max_itr and tol < delta_f[-1]:
    
    print("\nIteration {}".format(itr + 1))

    # Initializing the kriging model
    sm = KRG(theta0=[1e-2], corr=corr, theta_bounds=[1e-6, 1e2], print_global=False)

    # Setting the training values
    sm.set_training_values(xtrain, ytrain)
    
    # Creating surrogate model
    sm.train()

    # Find the minimum of surrogate model
    result = minimize(Exploitation(sm), algorithm, verbose=False)
    
    # Computing true function value at infill point
    y_infill = modified_branin(result.X.reshape(1,-1))

    if itr == 0:
        delta_f = [np.abs(result.F - y_infill)/np.abs(result.F)]
    else:
        delta_f = np.append(delta_f, np.abs(result.F - y_infill)/np.abs(result.F))
    
    print("Change in f: {}".format(delta_f[-1]))
    print("f*: {}".format(y_infill))
    print("x*: {}".format(result.X))
    
    # Appending the the new point to the current data set
    xtrain = np.vstack(( xtrain, result.X.reshape(1,-1) ))
    ytrain = np.append( ytrain, y_infill )
    
    itr = itr + 1 # Increasing the iteration number

# Printing the final results
print("\nBest obtained point:")
print("x*: {}".format(xtrain[np.argmin(ytrain)]))
print("f*: {}".format(np.min(ytrain)))

Iteration 1
Change in f: [1.28541756]
f*: [19.73821152]
x*: [1.2960495  3.34626052]

Iteration 2
Change in f: 0.008509034251574791
f*: [17.87623602]
x*: [1.63494873 4.30630427]

Iteration 3
Change in f: 0.05445549072274073
f*: [16.8471014]
x*: [1.89362037 4.10153672]

Iteration 4
Change in f: 0.01949037676331771
f*: [15.27545516]
x*: [2.58121384 3.46173263]

Iteration 5
Change in f: 0.07934021181583842
f*: [16.2587589]
x*: [2.87659199 3.55971802]

Iteration 6
Change in f: 0.014860955690321273
f*: [14.80534439]
x*: [2.63898464 2.54137866]

Iteration 7
Change in f: 5.471398515141134e-05
f*: [14.7798789]
x*: [2.63781264 2.701596  ]

Best obtained point:
x*: [2.63781264 2.701596  ]
f*: 14.779878904081613

Below block of code plots the convergence of the exploitation process.

####################################### Plotting convergence history

fig, ax = plt.subplots(1, 2, figsize=(14,6))
ax[0].plot(np.arange(itr) + 1, xtrain[num_train:,0], c="black", label='$x_1^*$', marker=".")
ax[0].plot(np.arange(itr) + 1, xtrain[num_train:,1], c="green", label='$x_2^*$', marker=".")
ax[0].plot(np.arange(itr) + 1, ytrain[num_train:], c="blue", label='$f^*$', marker=".")
ax[0].set_xlabel("Iterations", fontsize=14)
ax[0].set_ylabel("$f(x^*)$ and ($x_1^*$, $x_2^*$)", fontsize=14)
ax[0].legend()
ax[0].set_xlim(left=1, right=itr)
ax[0].grid()

ax[1].plot(np.arange(itr) + 1, delta_f, c="red", marker=".")
ax[1].plot(np.arange(itr+1), [tol]*(itr+1), c="black", linestyle="--", label="Tolerance")
ax[1].set_xlabel("Iterations", fontsize=14)
ax[1].set_ylabel(r"$| \hat{f}^* - f(x^*) | / | \hat{f}^* |$", fontsize=14)
ax[1].set_xlim(left=1, right=itr)
ax[1].grid()
ax[1].legend()
ax[1].set_yscale("log")

fig.suptitle("Exploitation".format(itr), fontsize=15)

Text(0.5, 0.98, 'Exploitation')

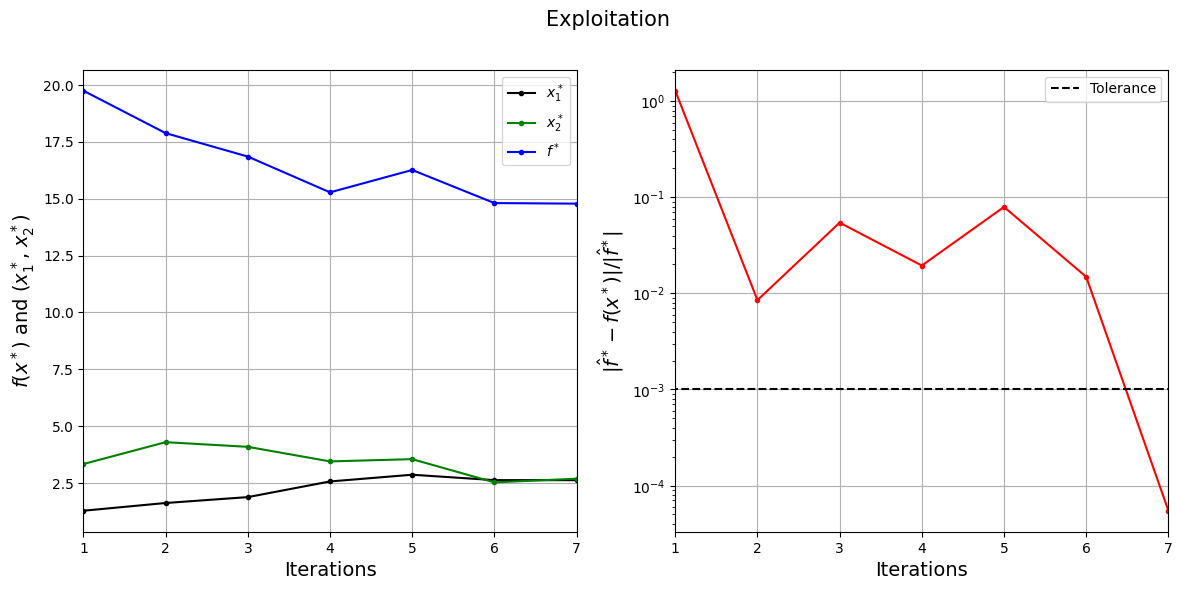
The figure on the left shows the history of infill points and corresponding true function values, and figure on the right shows the convergence of exploitation process. At the start, the infill points are added at different locations since the surrogate model is changing which results in different minima. As the number of iterations increases, the new infill points are added very close to the previous infill points since the surrogate minimum is more or less same. Also, notice that process stopped before reaching maximum number of infills since the convergence criteria was met.

Below block of code plots the infill points.

####################################### Plotting initial samples and infills

# Reshaping into grid
reshape_size = int(np.sqrt(num_plot))
X = xplot[:,0].reshape(reshape_size, reshape_size)
Y = xplot[:,1].reshape(reshape_size, reshape_size)
Z = yplot.reshape(reshape_size, reshape_size)

# Level
levels = np.linspace(-17, -5, 5)
levels = np.concatenate((levels, np.linspace(0, 30, 7)))
levels = np.concatenate((levels, np.linspace(35, 60, 5)))
levels = np.concatenate((levels, np.linspace(70, 300, 12)))

fig, ax = plt.subplots(figsize=(8,6))
CS=ax.contour(X, Y, Z, levels=levels, colors='k', linestyles='solid', alpha=0.5, zorder=-10)
ax.clabel(CS, inline=1, fontsize=8)
ax.scatter(xtrain[0:num_train,0], xtrain[0:num_train,1], c="red", label='Initial samples')
ax.scatter(xtrain[num_train:,0], xtrain[num_train:,1], c="black", label='Infills')
ax.plot(-3.689, 13.630, 'g*', markersize=15, label="Global minimum")
ax.plot(xtrain[np.argmin(ytrain)][0], xtrain[np.argmin(ytrain)][1], 'bo', label="Obtained minimum")
ax.legend()
ax.set_xlabel("$x_1$", fontsize=14)
ax.set_ylabel("$x_2$", fontsize=14)
ax.set_title("Modified Branin function", fontsize=15)

Text(0.5, 1.0, 'Modified Branin function')

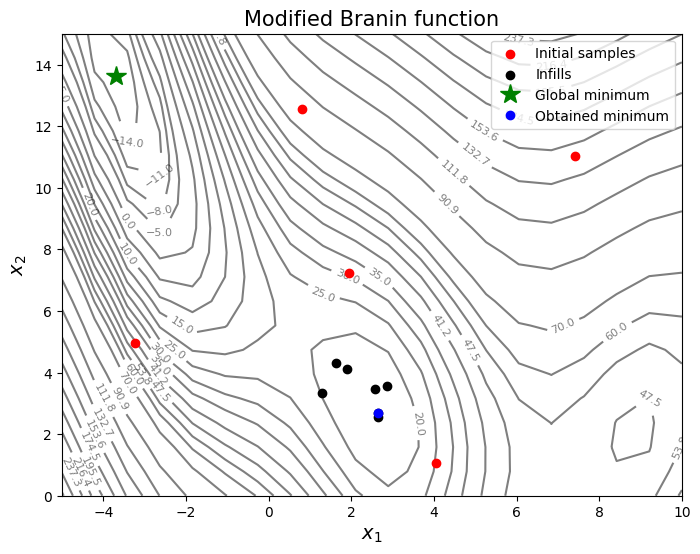
As can be seen in above plot, most of the points are added close to one of the local optimum which demonstrates exploitation only and no exploration. Due to this, exploitation process may get stuck in local optima and will not be able to find the global optimum. So, it is important to balance exploitation and exploration.

NOTE: Due to randomness in differential evolution, results may vary slightly between runs. So, it is recommend to run the code multiple times to see average behavior.

Final result:

Parameter	True minimum	Obtained minimum
\(x_1^*\)	-3.689	2.638
\(x_2^*\)	13.630	2.702
\(f(x_1^*, x_2^*)\)	-16.644	14.779